你每天都那么努力,忍受了那么多的寂寞和痛苦。可我也没见你有多优秀。
当我还是一个年轻男孩的时候画的一张关于树的画。
当你第一次学习编码时,大部分人都是将数组作为主要数据结构来学习。
之后,你将会学习到哈希表。如果你是计算机专业的,你肯定需要选修一门数据结构的课程。上课时,你又会学习到链表,队列和栈等数据结构。这些都被统称为线性的数据结构,因为它们在逻辑上都有起点和终点。
当你开始学习树和图的数据结构时,你会觉得它是如此的混乱。因为它的存储方式不是线性的,它们都有自己特定的方式存储数据。
这篇文章帮助你更好的理解树形数据结构并尽可能的帮你解决你的疑问。本章我们将学到
- 是什么是树?
- 一个简单树的例子
- 树的术语和工作原理
- 如何在代码中实现树结构
定义
当学习编程时,我们更容易理解线性的数据结构而不是树和图的数据结构。
树是众所周知的非线性数据结构。它们不以线性方式存储数据。他们按层次组织数据。
我们来举例一个现实生活中的例子
我们所说的层次组织到底是是什么呢?
想象一下我们的家谱:祖父母,父母,子女,兄弟姐妹等等,我们通常按层次结构组织家谱。
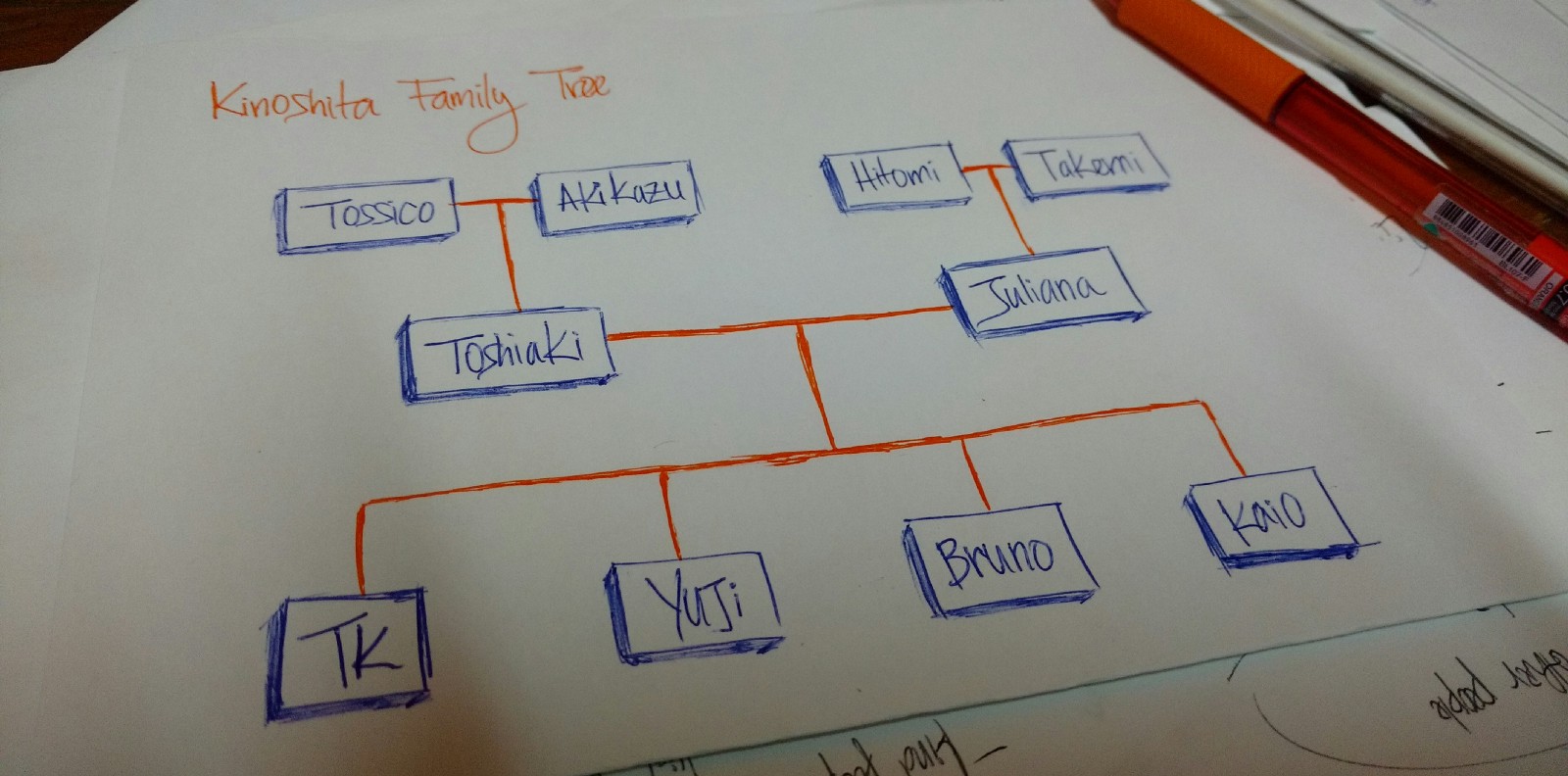
我的家庭族谱
上图是我的家谱。tossico,akikazu,hitomi和takemi是我的祖父母。
Toshiaki 和 Juliana 是我的父母。
TK 、Yuji 、Bruno 和 Kaio 是我父母的孩子(我和我的兄弟们)。
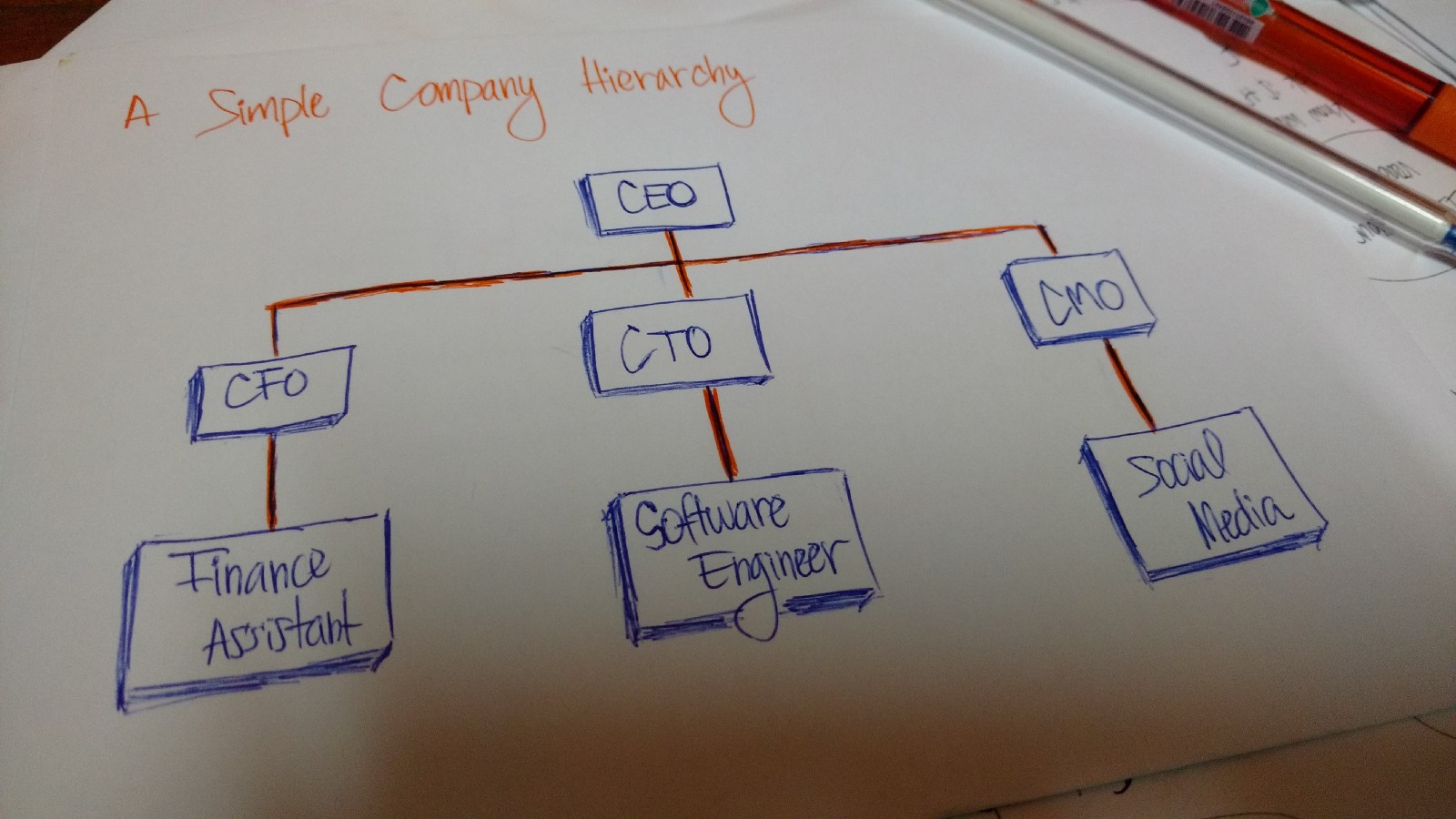
另一个层次结构的例子是企业的组织结构。
公司的结构也是是一个层次结构的例子
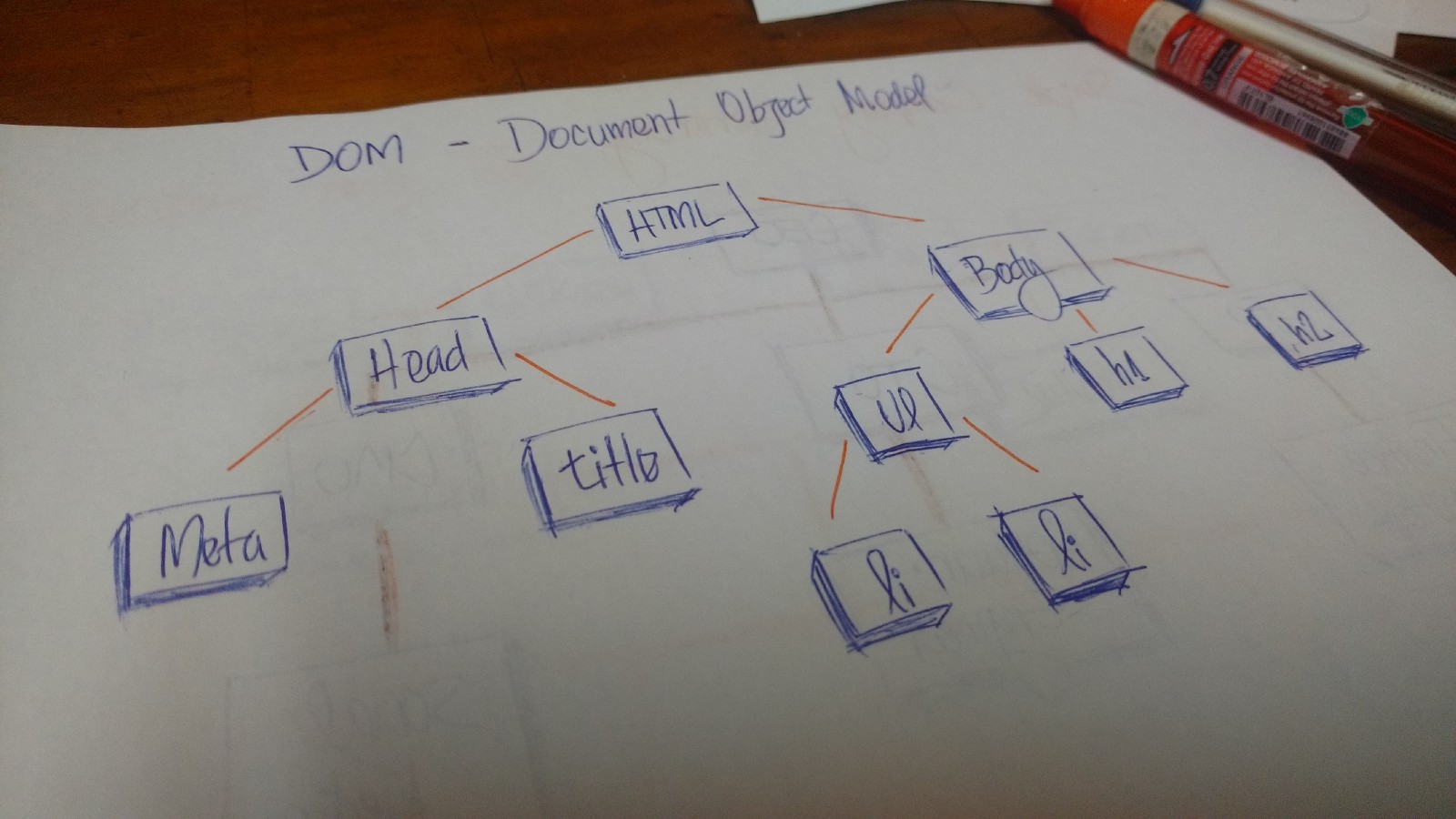
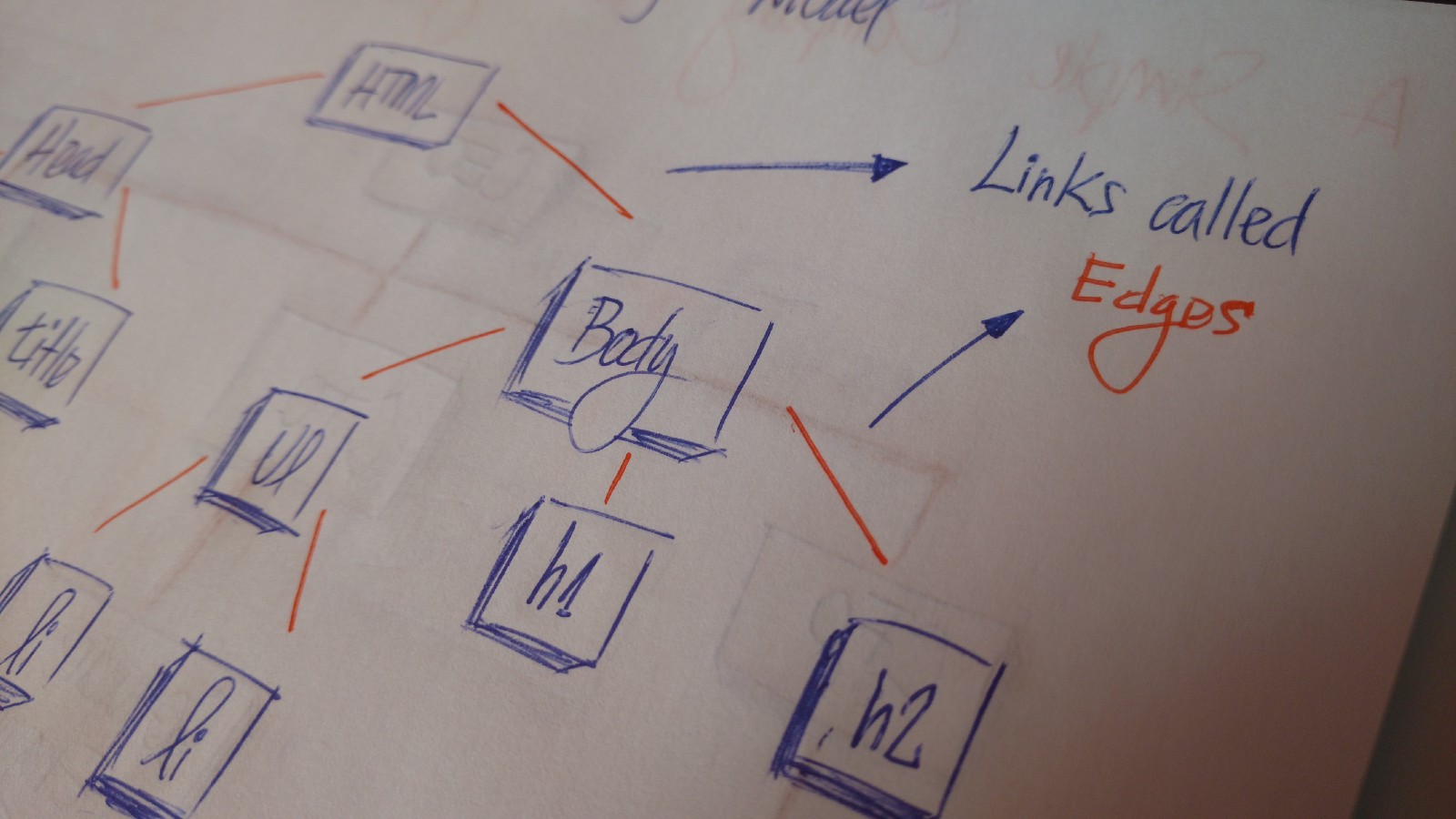
在 HTML 中,文档对象模型(DOM)是树形结构的。
文档对象模型(dom)
HTML 标签包含其他的标签。我们有一个 head 标签和 body 标签。这些标签包含特点的元素。head 标签中有 meta 和 title 标签。body 标签中有在用户界面展示的标签,如 h1 、a 、li 等等。
树的术语定义
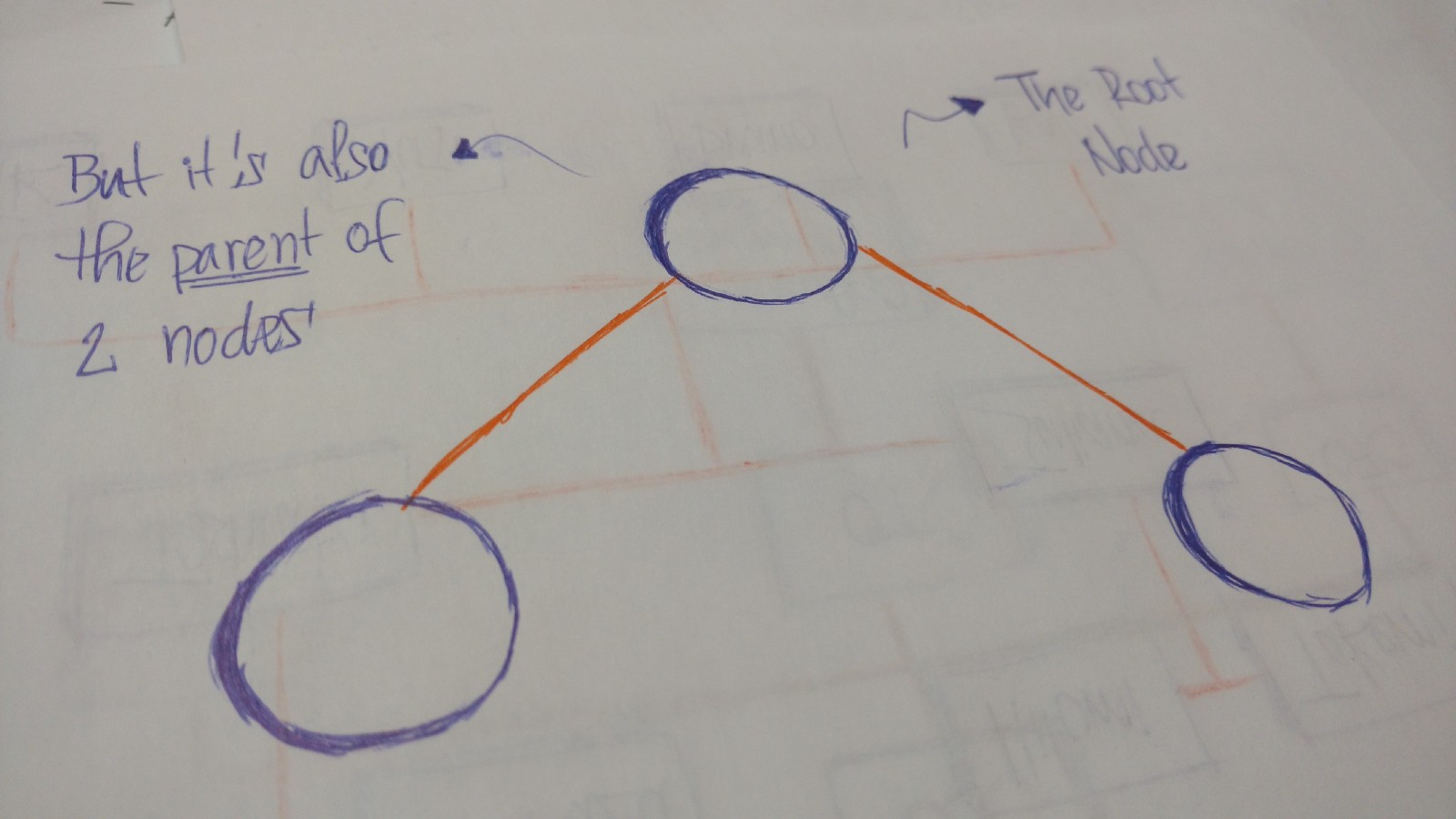
树(tree)是被称为结点(node)的实体的集合。结点通过边(edge)连接。每个结点都包含值或数据(value/date),并且每结节点可能有也可能没有子结点。
树的首结点叫根结点(即root结点)。如果这个根结点和其他结点所连接,那么根结点是父结点(parent node,与根结点连接的是子结点(child node)。
所有的结点都通过边(edge)连接。它是树中很重要得一个概念,因为它负责管理节点之间的关系。
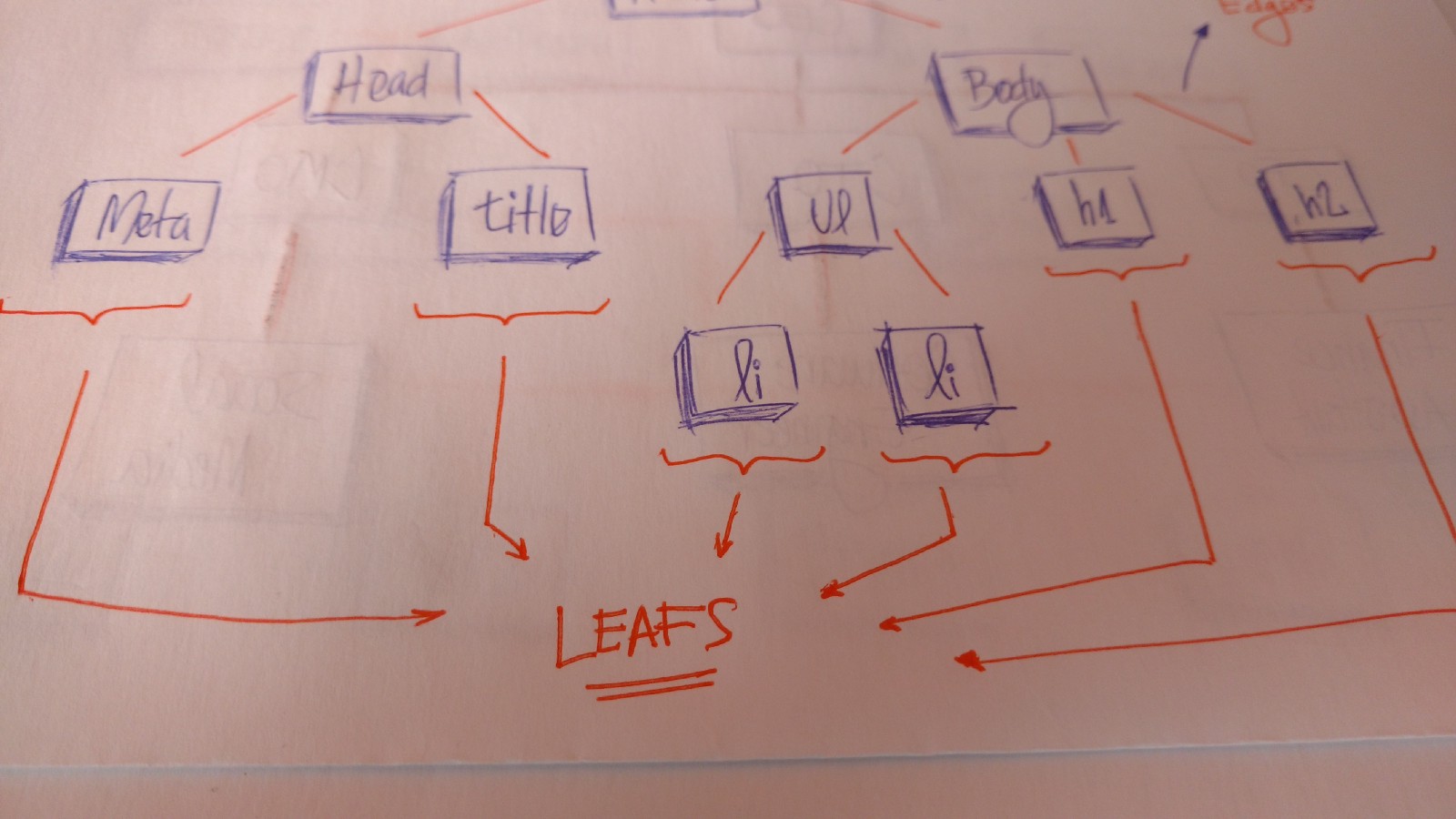
叶子结点(leaves)是树末端,它们没有子结点。像真正的大树一样,我们可以看到树上有根、枝干和树叶。
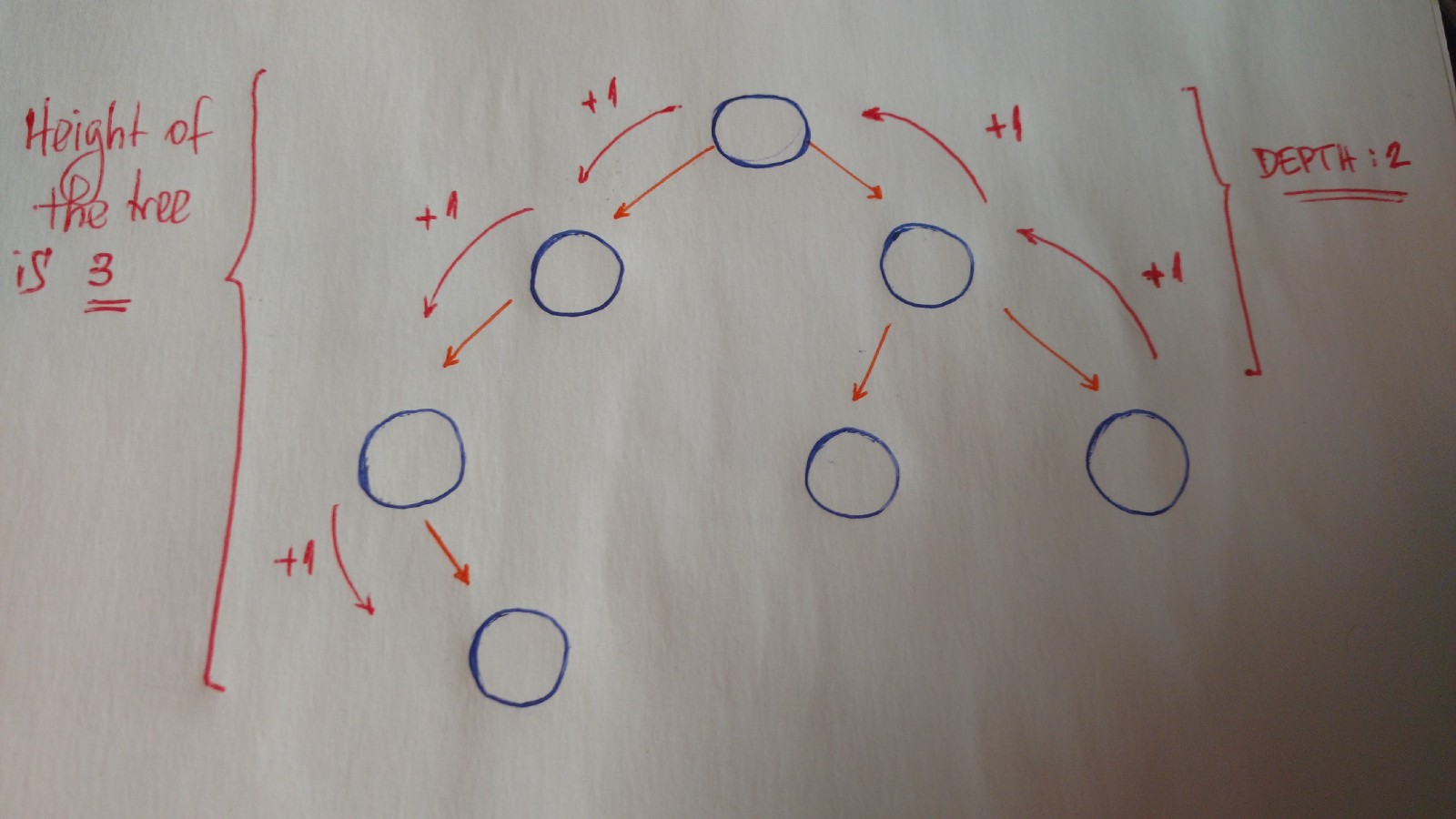
树的高度(height)和深度(depth)
- 树的高度是到叶子结点(树末端)的长度
- 结点的深度是它到根结点的长度
术语汇总
- 根结点是树最顶层结点
- 边是两个结点之间的连接
- 子结点是具有父结点的结点
- 父结点是与子结点有连接的结点
- 叶子结点是树中没有子结点的结点(树得末端)
- 高度是树到叶子结点(树得末端)的长度
- 深度是结点到根结点的长度
二叉树
现在我们来讨论一个特殊的树类型。我们把它叫作二叉树。
“在计算机科学领域,二叉树是一种树形数据结构,它的每个节点最多有两个孩子,被叫作左孩子和右孩” — Wikipedia
我们来写一个二叉树
当我们要实现二叉树时,我们需要牢记的第一件事是它是一个结点集合。每个结点都有三个属性:value,left_child和right_child。
那么我们怎么才能实现一个有这三个属性的简单二叉树呢?
我们来实现一个二叉树的例子
/**
* Created on 2018/4/16.
*
* @author zlf
* @since 1.0
*/
public class BinaryTree {
public BinaryTree left; //左节点
public BinaryTree right; //右节点
public String data; //树的内容
public BinaryTree() {
}
/**
* 构造方法
*
* @param data
* @param left
* @param right
*/
public BinaryTree(String data, BinaryTree left, BinaryTree right) {
this.left = left;
this.right = right;
this.data = data;
}
/**
* 构造方法
*
* @param data
*/
public BinaryTree(String data) {
this(data, null, null);
}
好,这就是我们的二叉树类
当我们实例化一个对象时,我们把值(点的相关数据)作为参数传递给类。看上面类的左孩子结点和右孩子结点。两个都被赋值为null。
为什么?
因为当我们创建节点时,它还没有孩子,只有结点数据。
代码测试
/**
* 构建树
*/
public static void testCreate() {
BinaryTree node = new BinaryTree("a");
System.out.println("【node data】:" + node.getData());
System.out.println("【node left data】:" + (node.left==null?"null":node.left.getData()));
System.out.println("【node right data】:" + (node.right==null?"null":node.right.getData()));
}
输出:
【node data】:a
【node left data】:null
【node right data】:null
我们可以将字符串’a’作为参数传给二叉树结点。如果将值、左孩子结点、右孩子结节点输出的话,我们就可以看到这个值了。
下面开始插入部分的操作。那么我们需要做些什么工作呢?
有两个要求:
-
如果当前的结点没有左孩子结点,我们就创建一个新结点,然后将其设置为当前结点的左结点。
-
如果已经有了左结点,我们就创建一个新结点,并将其放在当前左结点的位置。然后再将原左结点值为新左结点的左结点。
图形如下:
下面是插入的代码:
/**
* 插入节点 ,如果当前的节点没有左节点,我们就创建一个新节点,然后将其设置为当前节点的左节点。
*
* @param node
* @param value
*/
public static void insertLeft(BinaryTree node, String value) {
if (node != null) {
if (node.left == null) {
node.setLeft(new BinaryTree(value));
}
} else {
BinaryTree newNode = new BinaryTree(value);
newNode.left = node.left;
node.left = newNode;
}
}
再次强调,如果当前结点没有左结点,我们就创建一个新结点,并将其置为当前结点的左结点。否则,就将新结点放在左结点的位置,再将原左结点置为新左结点的左结点。
同样,我们编写插入右结点的代码
/**
* 同插入左结点
* @param node
* @param value
*/
public static void insertRight(BinaryTree node, String value) {
if (node != null) {
if (node.right == null) {
node.setRight(new BinaryTree(value));
}
} else {
BinaryTree newNode = new BinaryTree(value);
newNode.right = node.right;
node.right = newNode;
}
}
但是这还不算完成。我们得测试一下。
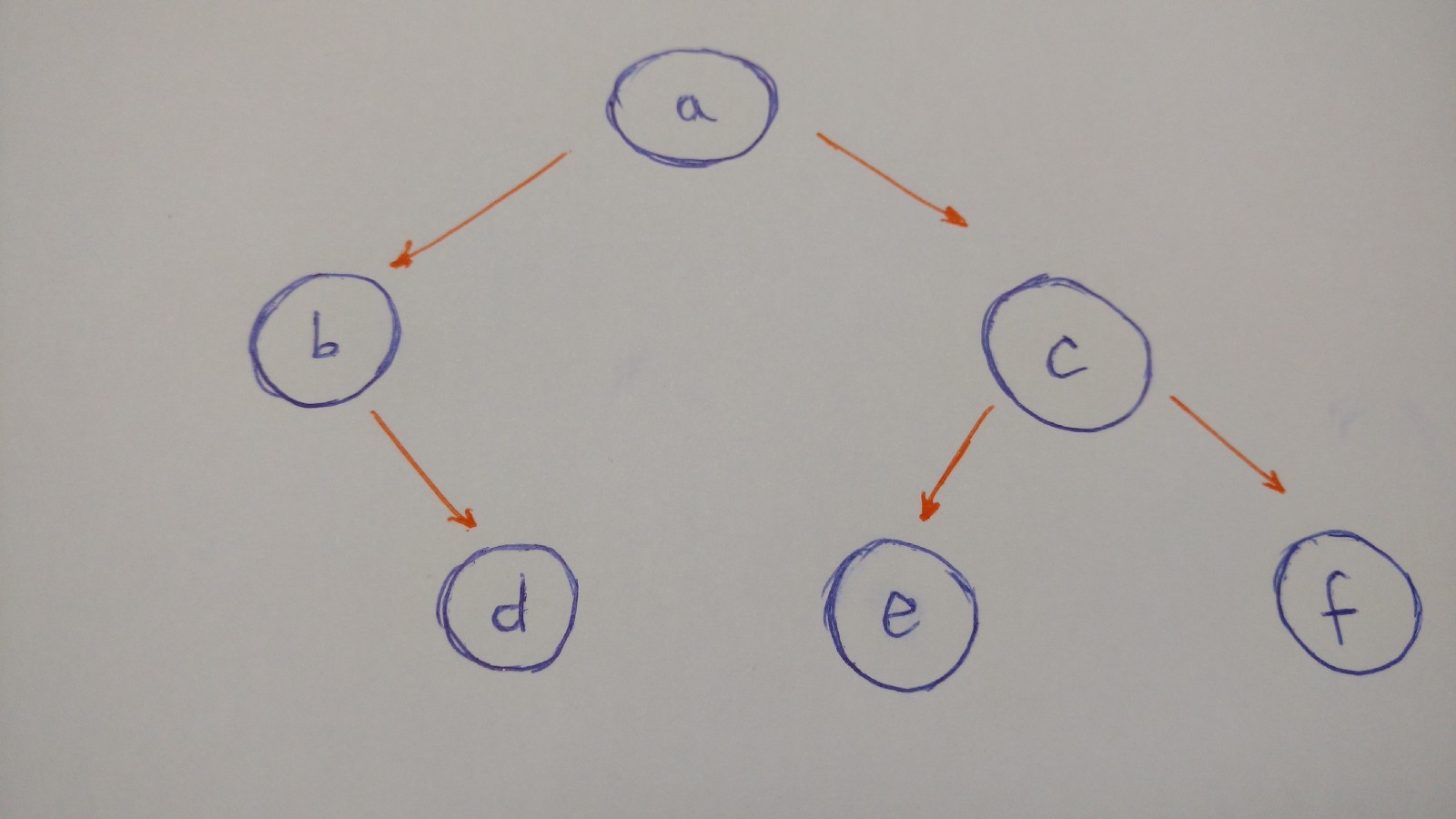
我们来构造一个像下面这样的树:
- 有一个根结点
- b是左结点
- c是右结点
- b的结节点是d(b没有左结点)
- c的左结点是e
- c的右结点是f
- e,f都没有子结点
下面是这棵树的实现代码:
/**
* 测试插入结点
*/
public static void testInsert() {
BinaryTree node_a = new BinaryTree("a");
node_a.insertLeft(node_a, "b");
node_a.insertRight(node_a, "c");
BinaryTree node_b = node_a.left;
node_b.insertRight(node_b, "d");
BinaryTree node_c = node_a.right;
node_c.insertLeft(node_c, "e");
node_c.insertRight(node_c, "f");
BinaryTree node_d = node_b.right;
BinaryTree node_e = node_c.left;
BinaryTree node_f = node_c.right;
System.out.println("【node_a data】:" + node_a.getData());
System.out.println("【node_b data】:" + node_b.getData());
System.out.println("【node_c data】:" + node_c.getData());
System.out.println("【node_d data】:" + node_d.getData());
System.out.println("【node_e data】:" + node_e.getData());
System.out.println("【node_f data】:" + node_f.getData());
}
输出:
【node_a data】:a
【node_b data】:b
【node_c data】:c
【node_d data】:d
【node_e data】:e
【node_f data】:f
插入已经结束
现在,我们来考虑一下树的遍历。
树的遍历有两种选择,深度优先搜索(DFS)和广度优先搜索(BFS)。
DFS是用来遍历或搜索树数据结构的算法。从根节点开始,在回溯之前沿着每一个分支尽可能远的探索。 — Wikipedia
BFS是用来遍历或搜索树数据结构的算法。从根节点开始,在探索下一层邻居节点前,首先探索同一层的邻居节点。 — Wikipedia
下面,我们来深入了解每一种遍历算法。
深度优先搜索(Depth-First Search,DFS)
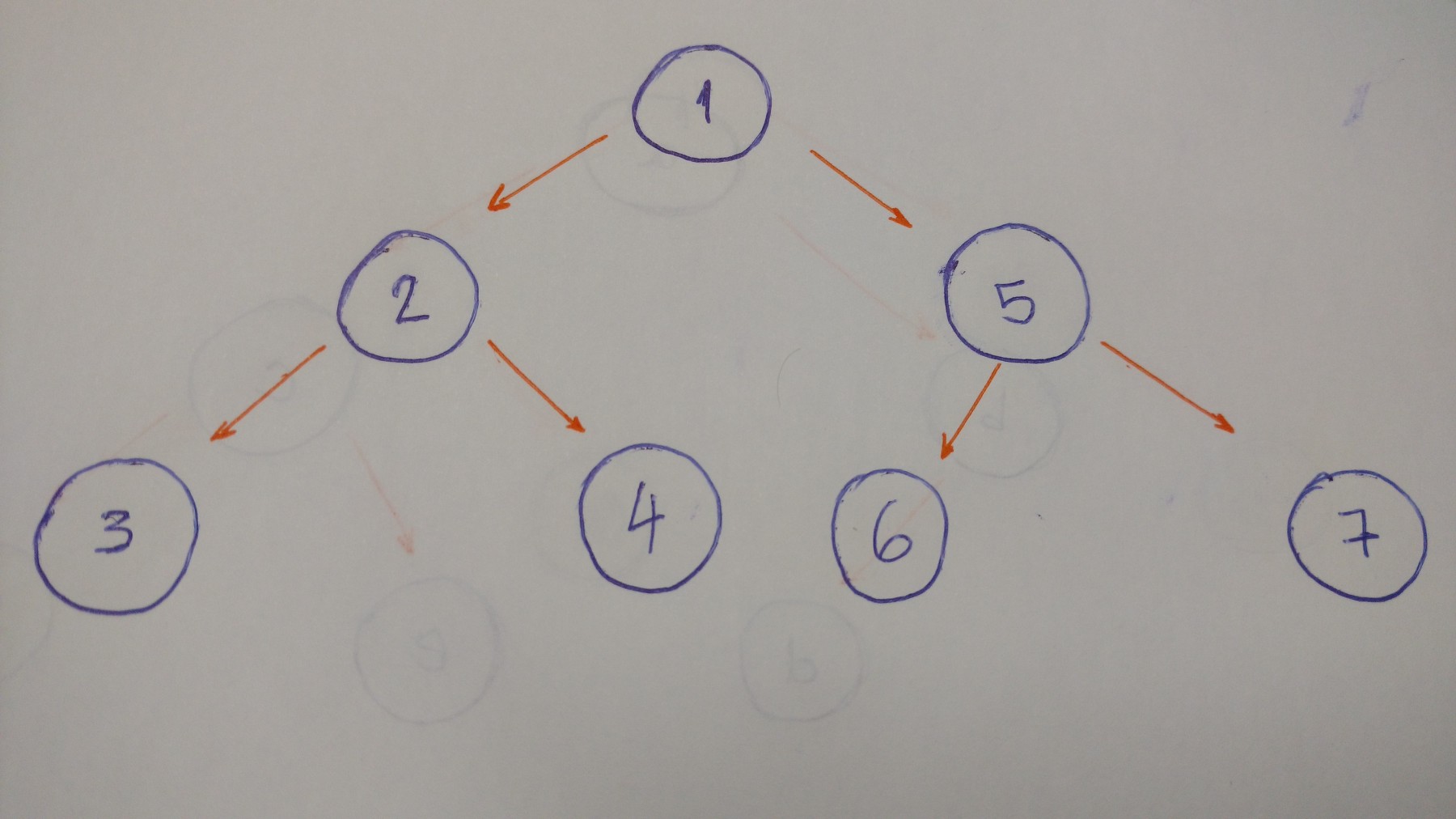
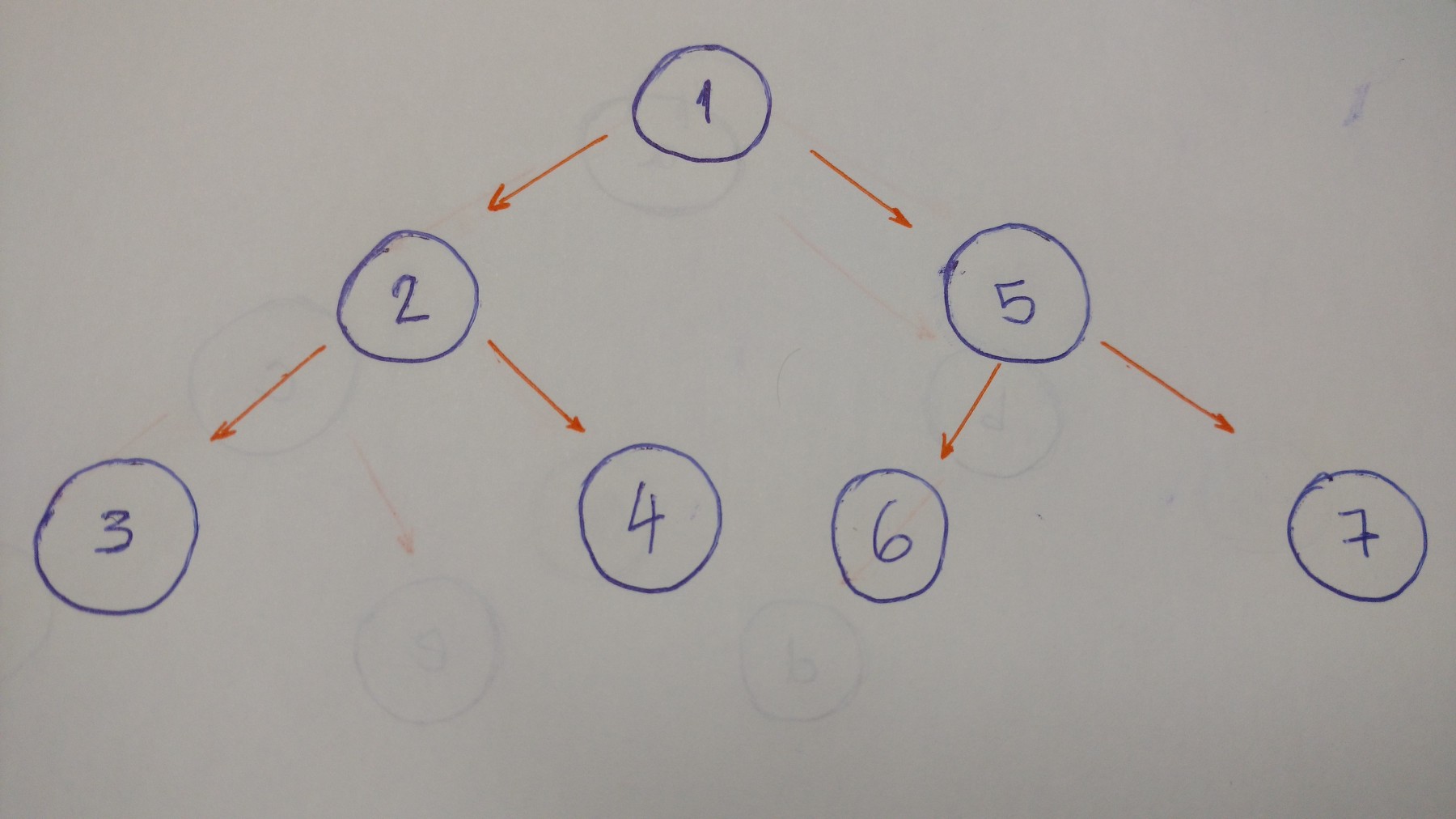
DFS 在回溯和搜索其他路径之前找到一条到叶节点的路径。让我们看看这种类型的遍历的示例。
输出结果为: 1–2–3–4–5–6–7
为什么?
让我们分解一下:
- 从根结点(1)开始。输出
- 进入左结点(2)。输出
- 然后进入左孩子(3)。输出
- 回溯,并进入右孩子(4)。输出
- 回溯到根结点,然后进入其右孩子(5)。输出
- 进入左孩子(6)。输出
- 回溯,并进入右孩子(7)。输出
- 完成
当我们深入到叶结点时回溯,这就被称为 DFS 算法。
既然我们对这种遍历算法已经熟悉了,我们将讨论下 DFS 的类型:前序、中序和后序。
前序遍历
这和我们在上述示例中的作法基本类似。
- 输出节点的值
- 进入其左结点并输出。当且仅当它拥有左结点。
- 进入右结点并输出之。当且仅当它拥有右结点
/**
* 前序遍历
*
* @param node
*/
public static void preOrder(BinaryTree node) {
if (node != null) {
System.out.println(node.data);
if (node.left != null) {
node.left.preOrder(node.left);
}
if (node.right != null) {
node.right.preOrder(node.right);
}
}
}
中序遍历
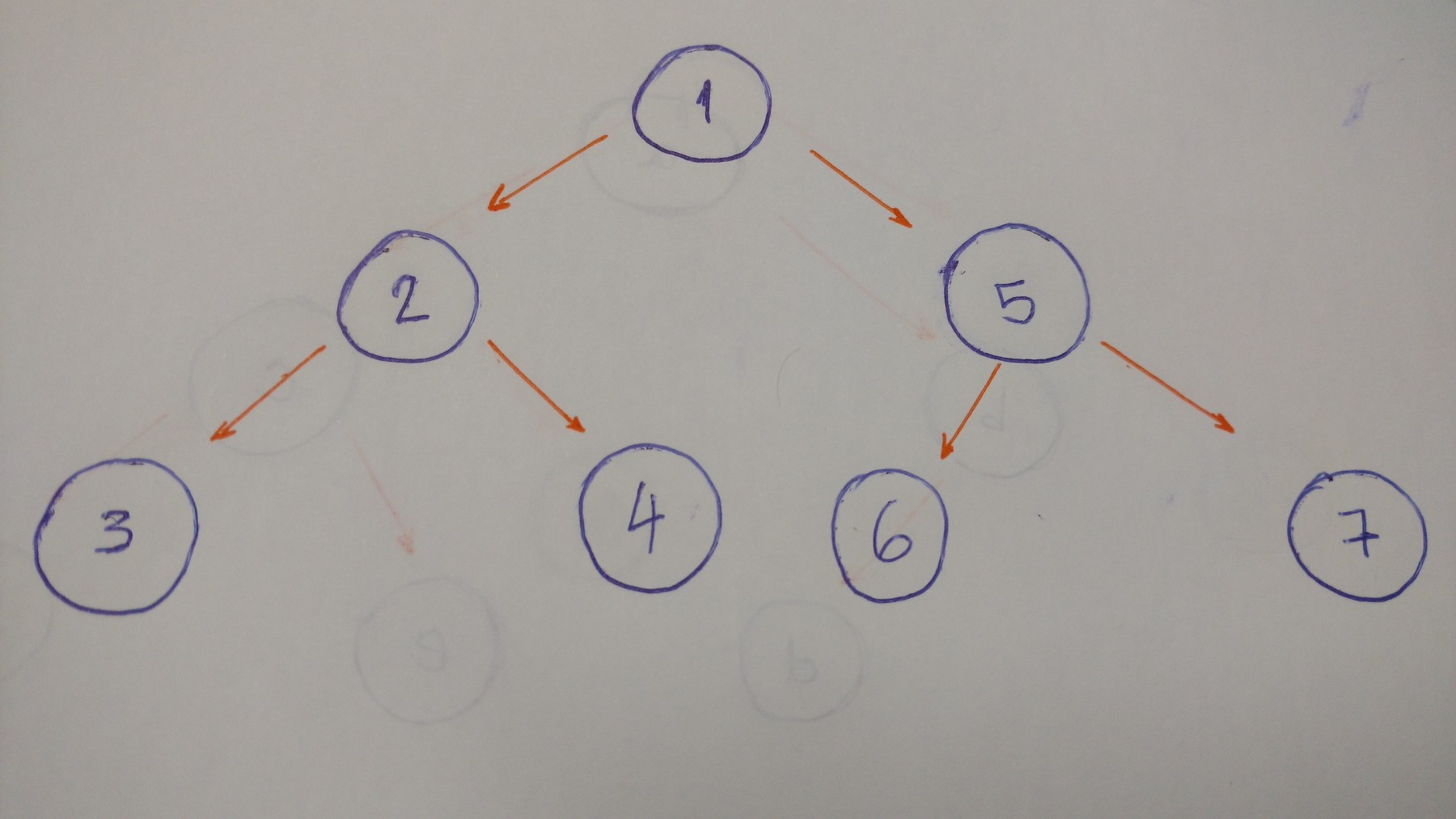
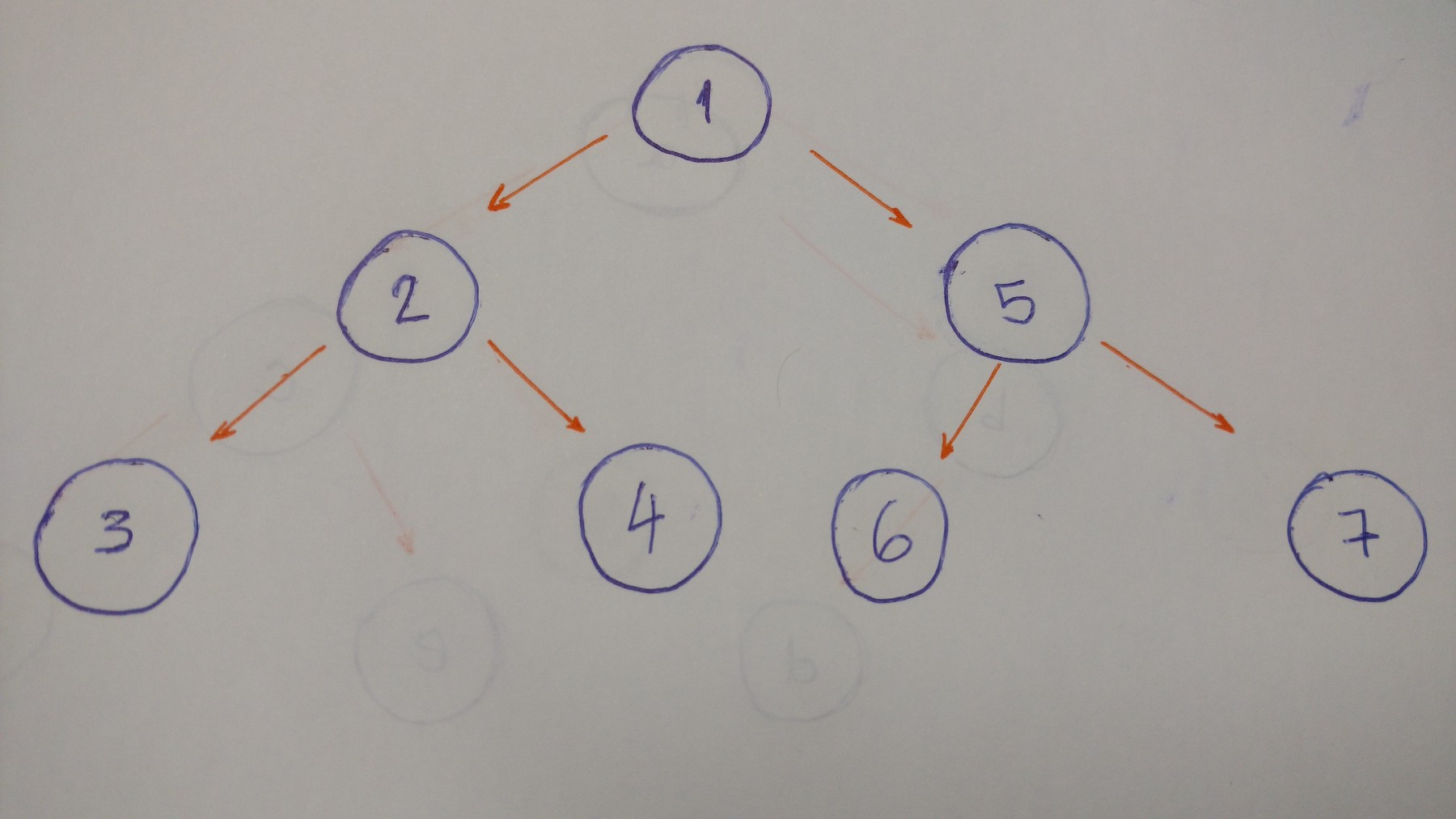
示例中此树的中序算法的结果是3–2–4–1–6–5–7。
左结点优先,之后是中间,最后是右结点。
代码实现:
/**
* 中序遍历
*
* @param node
*/
public static void inOrder(BinaryTree node) {
if (node != null) {
if (node.left != null) {
node.left.inOrder(node.left);
}
System.out.println(node.data);
if (node.right != null) {
node.right.inOrder(node.right);
}
}
}
- 进入左结点并输出之。当且仅当它有左结点。
- 输出根结点的值。
- 进入结节点并输出之。当且仅当它有结节点。
后序遍历
以此树为例的后序算法的结果为 3–4–2–6–7–5–1 。
左结点优先,之后是右结点,根结点的最后。
代码实现:
/**
* 后序遍历
*
* @param node
*/
public static void postOrder(BinaryTree node) {
if (node != null) {
if (node.left != null) {
node.left.postOrder(node.left);
}
if (node.right != null) {
node.right.postOrder(node.right);
}
System.out.println(node.data);
}
}
- 进入左结点输出,
- 进入右结点输出
- 输出根结点
广度优先搜索(BFS)
BFS是一层层逐渐深入的遍历算法
下面这个例子是用来帮我们更好的解释该算法。
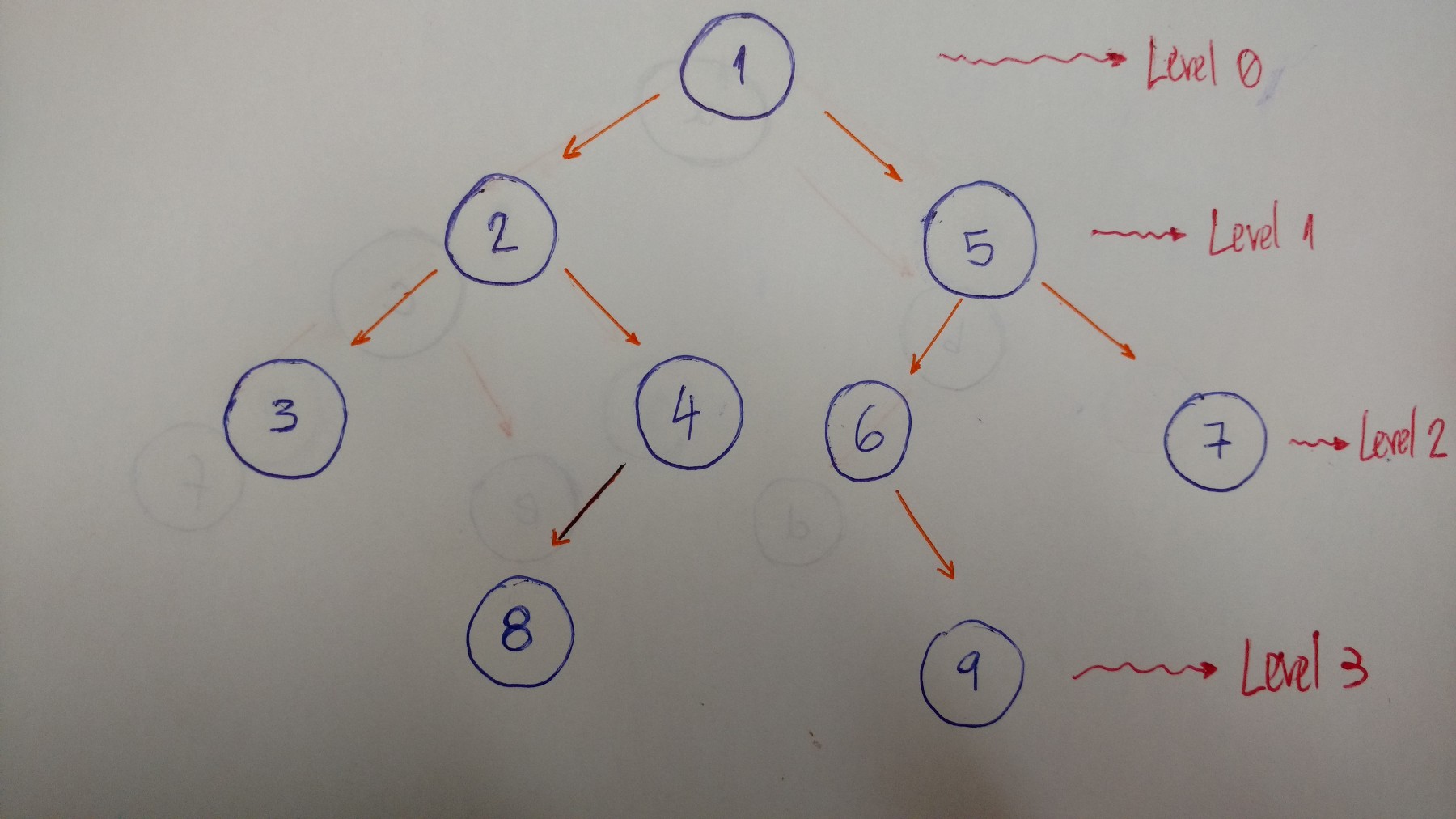
我们来一层一层的遍历这棵树。本例中,就是1-2-5-3-4-6-7.
- 0层/深度0:只有值为1的结点
- 1层/深度1:有值为2和5的结点
- 2层/深度2:有值为3、4、6、7的结点
代码实现:
/**
* 广度排序
*
* @param node
*/
public static void bfsOrder(BinaryTree node) {
if (node != null) {
Queue<BinaryTree> queue = new ArrayDeque<BinaryTree>();
queue.add(node);
while (!queue.isEmpty()) {
BinaryTree current_node = queue.poll();
System.out.println(current_node.data);
if (current_node.left != null) {
queue.add(current_node.left);
}
if (current_node.right != null) {
queue.add(current_node.right);
}
}
}
}
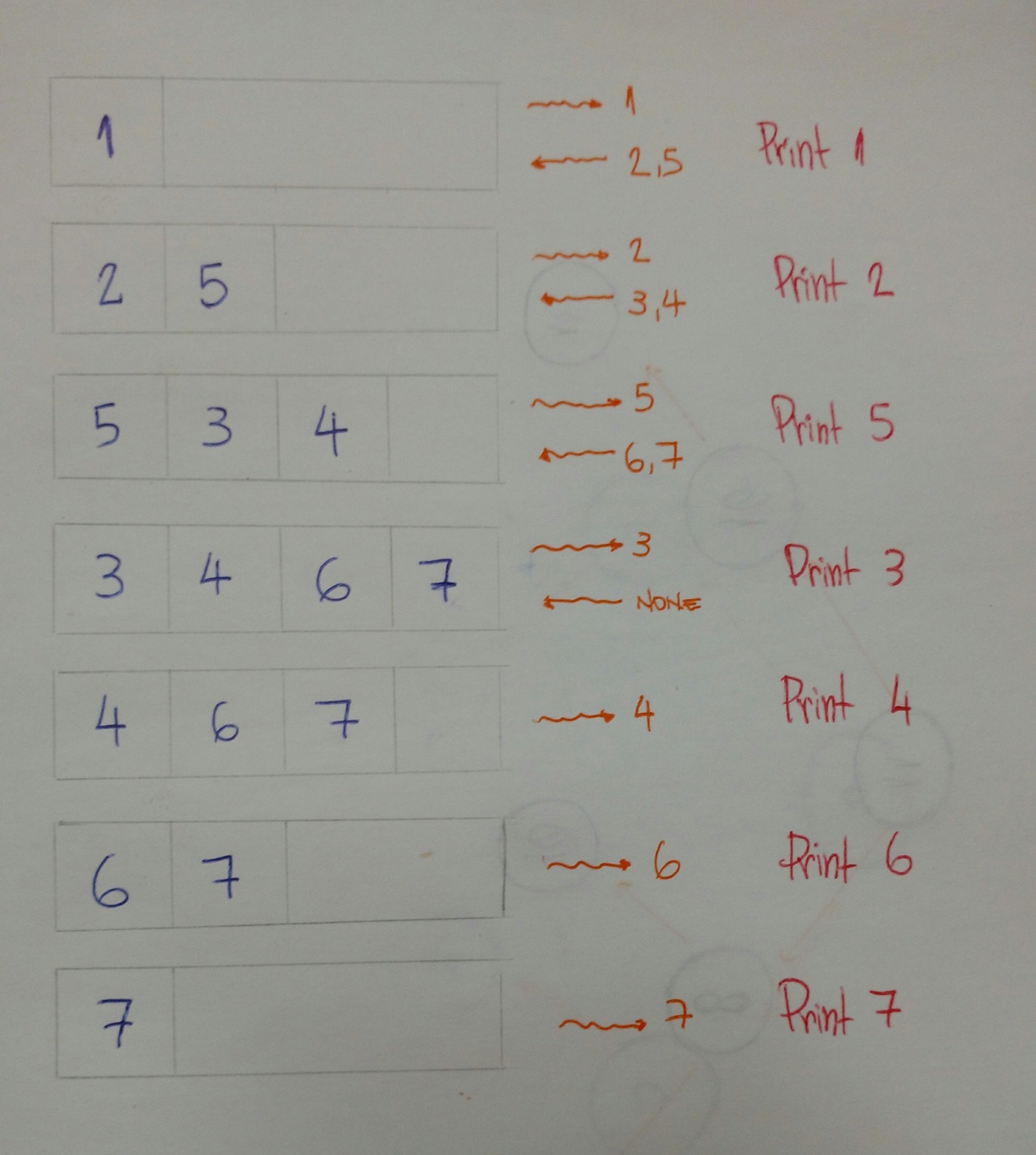
为了实现BFS算法,我们需要用到一个数据结构,那就是队列。
队列具体是用来干什么的呢?
请看下面解释。
- 首先用add方法将根结点添加到队列中。
- 当队列不为空时迭代。
- 获取队列中的第一个结点,然后输出其值
- 将左节点和右结点添加到队列
- 在队列的帮助下我们将每一个结点值一层层输出
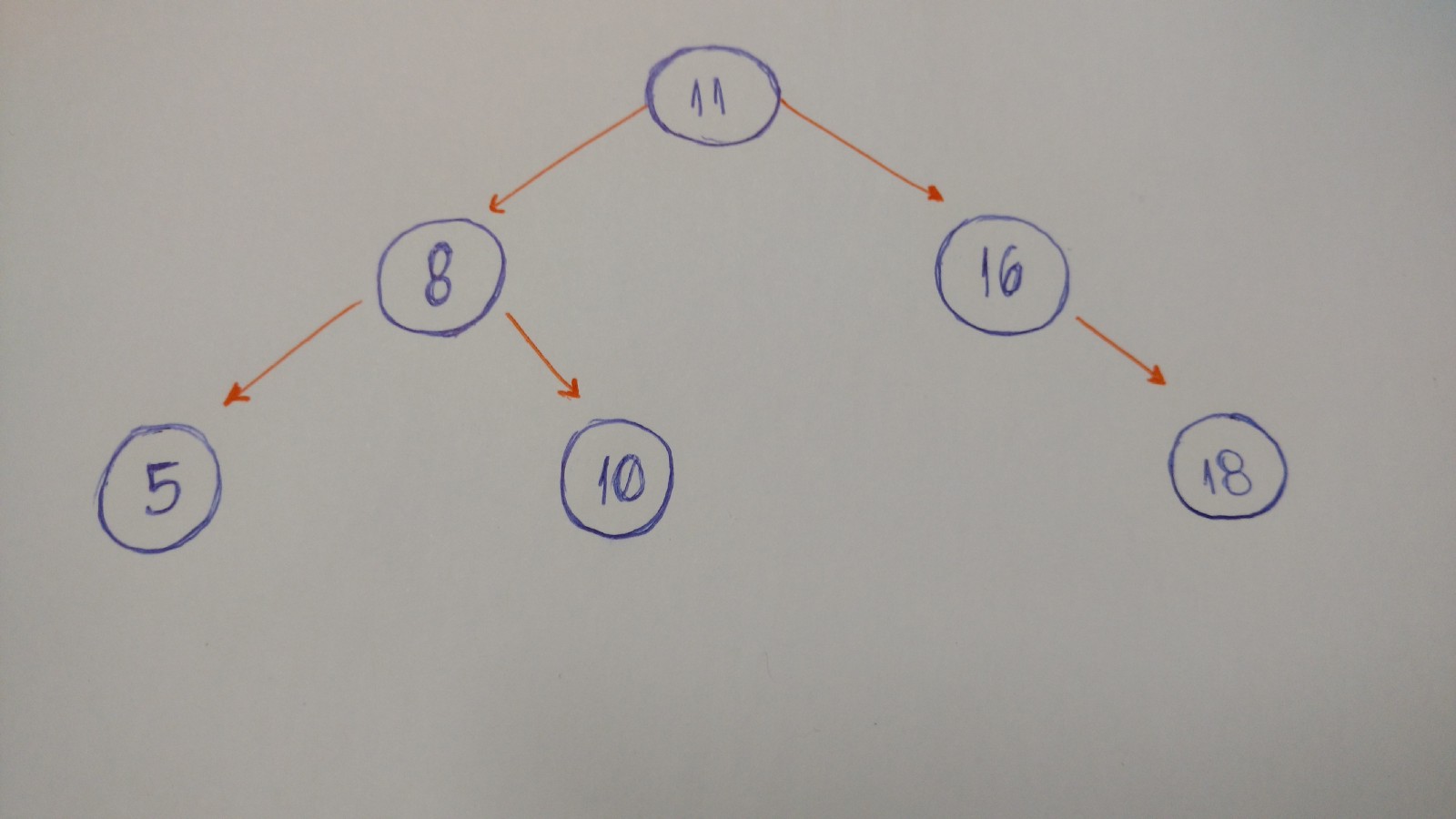
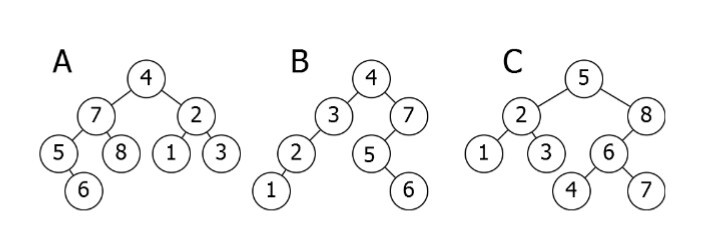
二叉搜索树
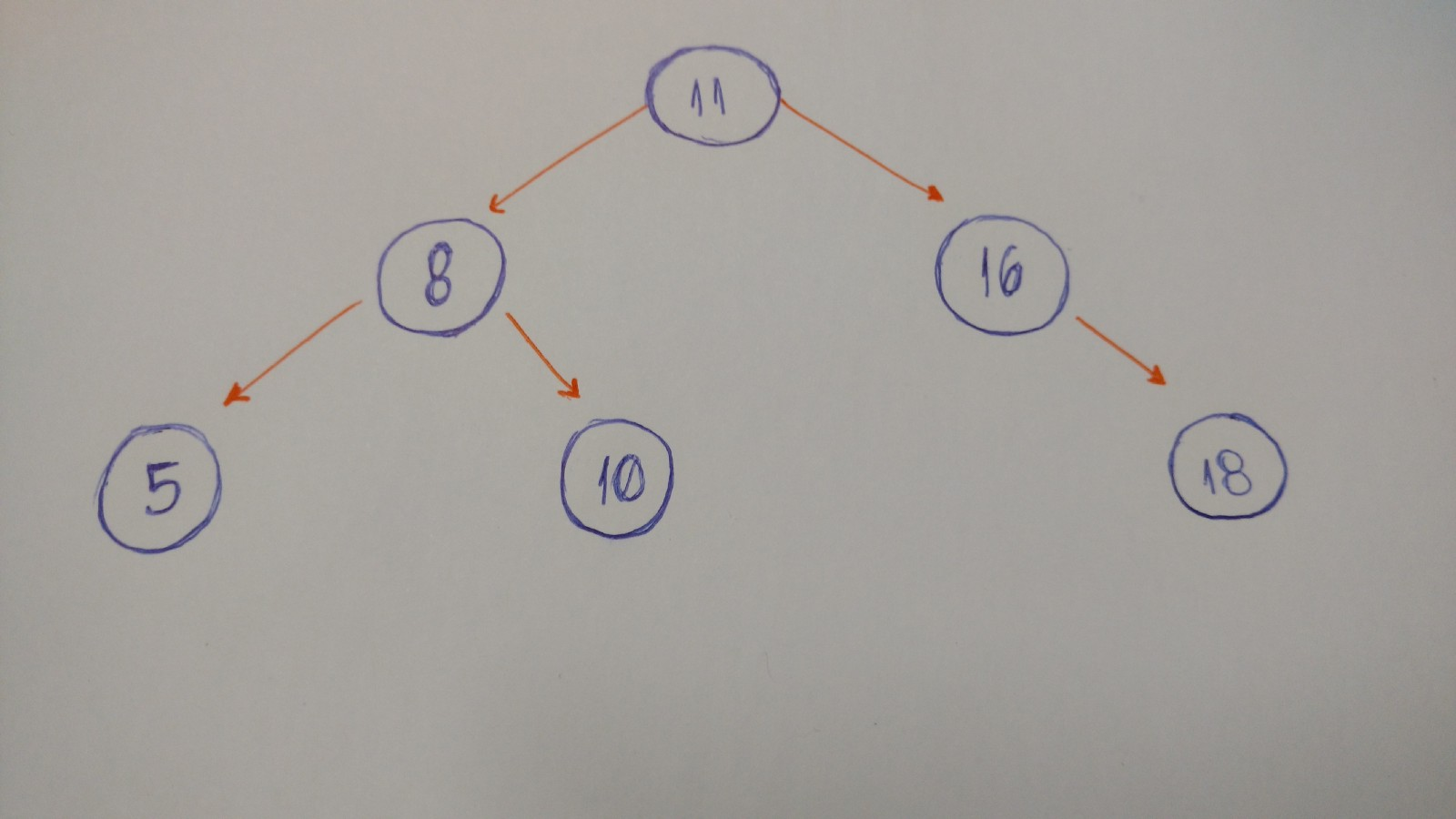
二叉搜索树有时候被称为二叉有序树或二叉排序树,二叉搜索树的值存储在有序的顺序中,因此,查找表和其他的操作可以使用折半查找原理。——Wikipedia
二叉搜索树中的一个重要性质是,二叉搜索树中一个节点的值大于其左结点,但是小于其右结点
- 是反的二叉搜索树。子树 7-5-8-6应该在右边,而子树2-1-3 应该在左边。
- 是唯一正确的选项。它满足二叉搜索树的性质
- 有一个问题:值为4的那个结点应该在根结点的左边,因为这个节点的值比根结点的值5小。
代码实现二叉树搜索
插入:向我们的树添加新的结点
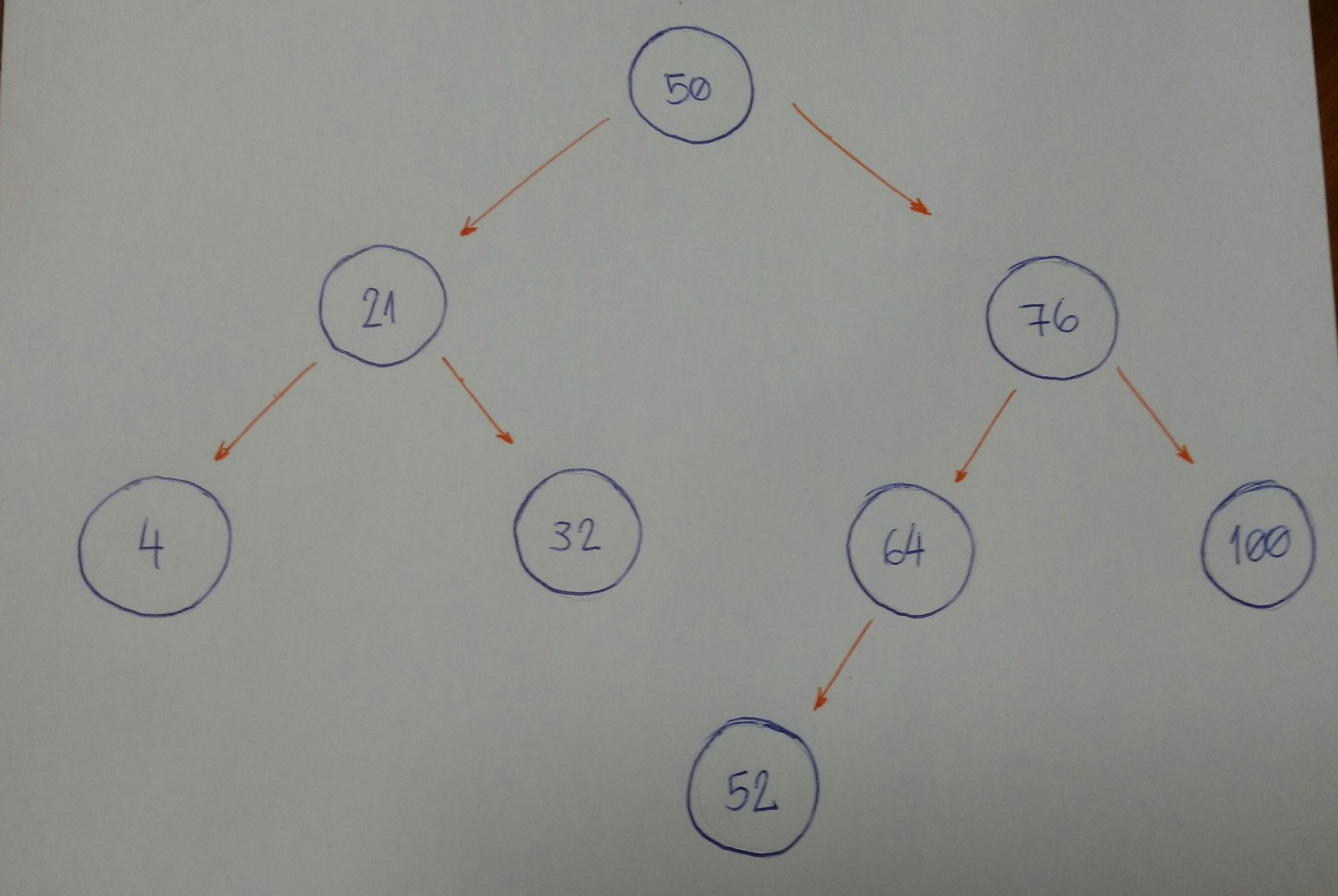
现在想像一下我们有一棵空树,我们想将几个节点添加到这棵空树中,这几个结点的值为:50、76、21、4、32、100、64、52。
首先我们需要知道的是,50是不是这棵树的根结点。
现在我们开始一个一个的插入结点
- 76比50大,所以76插入在右边。
- 21比50小,所以21插入在左边。
- 4比50小。但是50已经有了值为21的左结点。然后,4又比21小,所以将其插入在21的左边。
- 32比50小。但是50已经有了值为21的左结点。然后,32又比21大,所以将其插入在21的右边。
- 100比50大。但是50已经有了一个值为76的右结点。然后,100又比76大,所以将其插入在76的右边。
- 64比50大。但是50已经有了一个值为76的右结点。然后,64又比76小,所以将其插入在76的左边。
- 52比50大。但是50已经有了一个值为76的右结点。52又比76小,但是76也有一个值为64左结点。52又比64小,所以将52插入在64的左边。
你注意到这里的模式了吗?
让我们把它分解。
- 新结点值大于当前节点还是小于当前结点?
- 如果新节点的值大于当前结点,则转到右结点。如果当前节点没有右结点,则在那里插入新结点,否则返回步骤1。
- 如果新节点的值小于当前结点,则转到左结点。如果当前节点没有左结点,则在那里插入新结点,否则返回步骤1。
- 这里我们没有处理特殊情况。当新节点的值等于结点的当前值时,使用规则3。考虑在子结点的左侧插入相等的值。
代码实现:
/**
* 插入树
*
* @param node
* @param value
*/
public void insertNode(BinaryTree node, Integer value) {
if (node != null) {
if (value <= Integer.valueOf(node.data) && node.left != null) {
node.left.insertNode(node.left, value);
} else if (value <= Integer.valueOf(node.data)) {
node.left = new BinaryTree(String.valueOf(value));
} else if (value > Integer.valueOf(node.data) && node.right != null) {
node.right.insertNode(node.right, value);
} else {
node.right = new BinaryTree(String.valueOf(value));
}
}
}
看起来很简单。
该算法的强大之处是其递归部分,即第9行和第13行。这两行代码均调用 insertNode 方法,并分别为其左结点和右结点使用它。第11行和第15行则在子结点处插入新结点。
搜索结点
我们现在要构建的算法是关于搜索的。对于给定的值(整数),我们会搜索出我们的二叉查找树有或者没有这个值。
需要注意的一个重要事项是我们如何定义树的插入算法。 首先我们有根结点。所有左子的节点值都比根结点小。所有右子树的节点值都比根结点大。
让我们看一个例子。
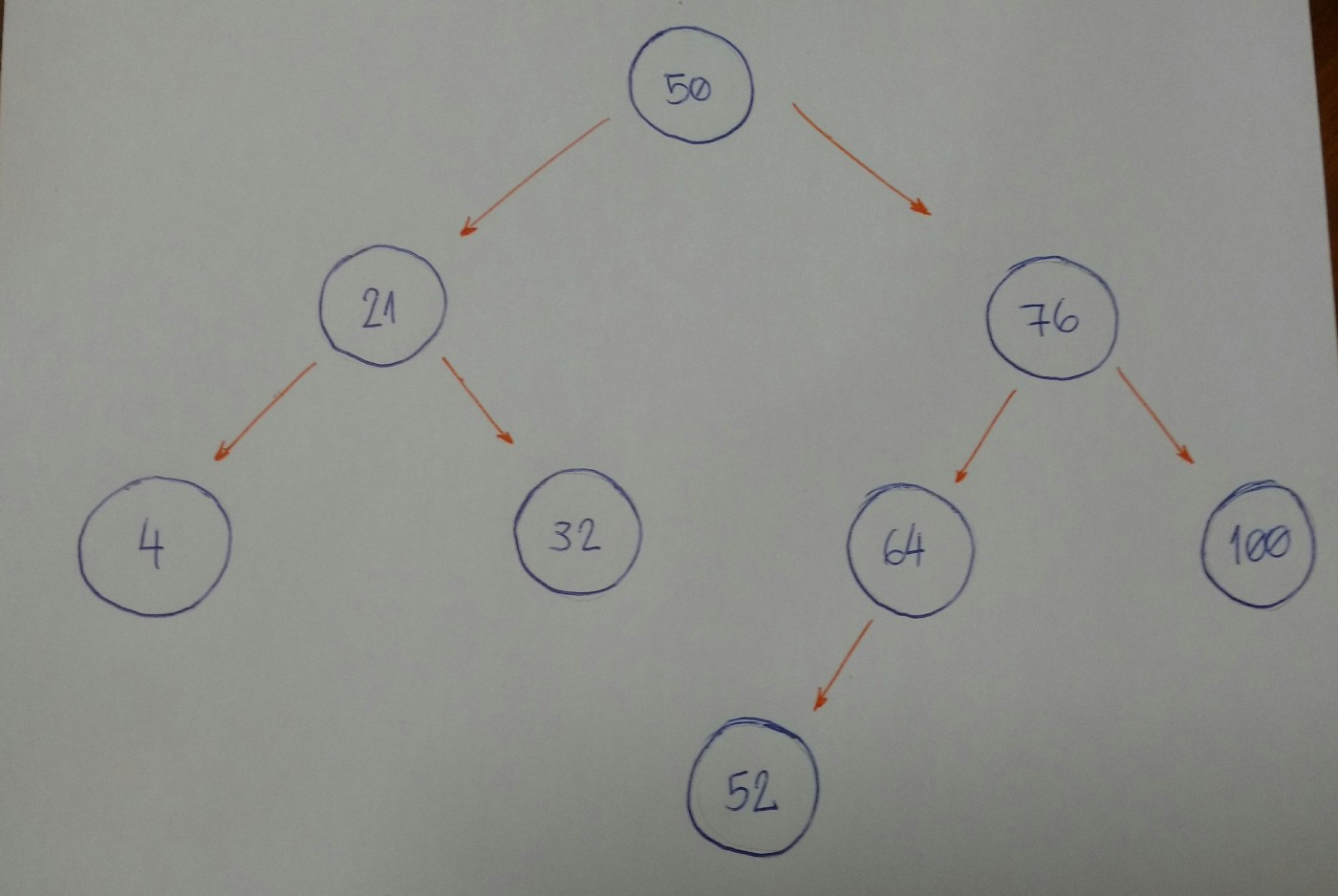
假设我们有这棵树。
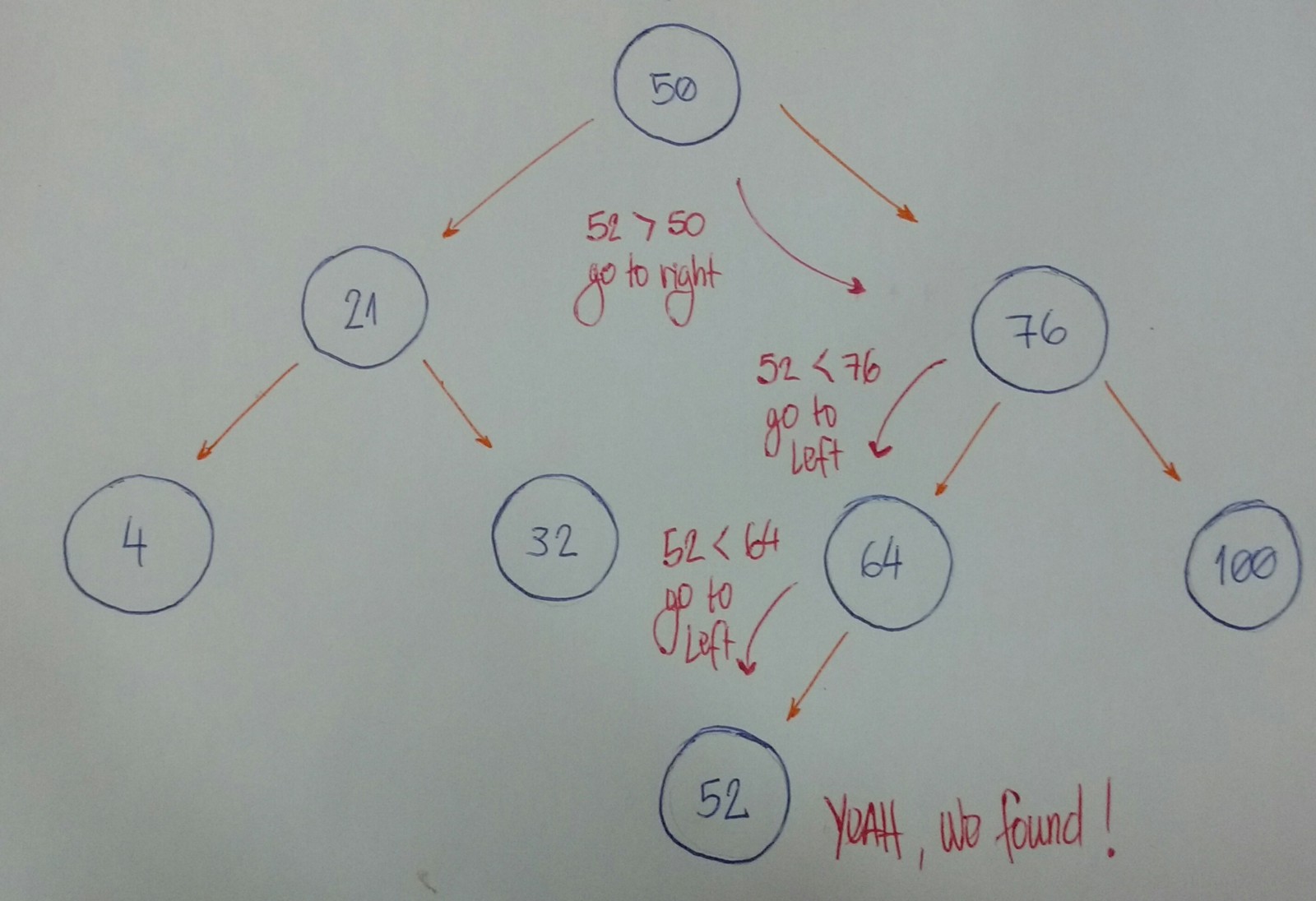
现在我们想知道是否有一个结点的值为52。
让我们把它分解。
- 我们以根结点作为当前节点开始。给定值小于当前结点值吗?如果是,那么我将在左子树上查找它。
- 给定值大于当前结点值吗?如果是,那么我们将在右子树上查找它。
- 如果规则 #1 和 #2 均为假,我们可以比较当前节点值和给定值是否相等。如果返回真,那么我们可以说:“是的,我们的树拥有给定的值。” 否则,我们说: “不,我们的树没有给定的值。”
代码实现:
/**
* 查找节点是否存在
*
* @param node
* @param value
* @return
*/
public boolean findNode(BinaryTree node, Integer value) {
if (node != null) {
if (value < Integer.valueOf(node.data) && node.left != null) {
return node.left.findNode(node.left, value);
}
if (value > Integer.valueOf(node.data) && node.right != null) {
return node.right.findNode(node.right, value);
}
return value == Integer.valueOf(node.data);
}
return false;
}
代码分析:
- 第8行和第9行归于规则#1。
- 第10行和第11行归于规则#2。
- 第13行归于规则#3。
删除:移除和重新组织树
删除是一个更复杂的算法,因为我们需要处理不同的情况。对于给定值,我们需要删除具有此值的结点。想象一下这个节点的以下场景:它没有孩子,有一个孩子,或者有两个孩子。
一个没有孩子的节点(叶节点) 。
# |50| |50|
# / \ / \
# |30| |70| (DELETE 20) ---> |30| |70|
# / \ \
# |20| |40| |40|
如果要删除的结点没有子结点,我们简单地删除它。该算法不需要重组树。
仅有一个孩子(左或右孩子)的结点。
# |50| |50|
# / \ / \
# |30| |70| (DELETE 30) ---> |20| |70|
# /
# |20|
在这种情况下,我们的算法需要使节点的父节点指向子结点。如果节点是左孩子,则使其父结点指向其子结点。如果结点是右孩子,则使其父结点指向其子结点。
有两个孩子的节点。
# |50| |50|
# / \ / \
# |30| |70| (DELETE 30) ---> |40| |70|
# / \ /
# |20| |40|
当节点有两个孩子,则需要从该节点的右孩子开始,找到具有最小值的结点。我们将把具有最小值的这个节点置于被删除的节点的位置。
代码实现:
/**
* 删除节点
* @param node
* @param value
* @param parent
* @return
*/
public boolean removeNode(BinaryTree node, Integer value, BinaryTree parent) {
if (node != null) {
if (value < Integer.valueOf(node.data) && node.left != null) {
return node.left.removeNode(node.left, value, node);
} else if (value < Integer.valueOf(node.data)) {
return false;
} else if (value > Integer.valueOf(node.data) && node.right != null) {
return node.right.removeNode(node.right, value, node);
} else if (value > Integer.valueOf(node.data)) {
return false;
} else {
if (node.left == null && node.right == null && node == parent.left) {
parent.left = null;
node.clearNode(node);
} else if (node.left == null && node.right == null && node == parent.right) {
parent.right = null;
node.clearNode(node);
} else if (node.left != null && node.right == null && node == parent.left) {
parent.left = node.left;
node.clearNode(node);
} else if (node.left != null && node.right == null && node == parent.right) {
parent.right = node.left;
node.clearNode(node);
} else if (node.right != null && node.left == null && node == parent.left) {
parent.left = node.right;
node.clearNode(node);
} else if (node.right != null && node.left == null && node == parent.right) {
parent.right = node.right;
node.clearNode(node);
} else {
node.data=String.valueOf(node.right.findMinValue(node.right));
node.right.removeNode(node.right,Integer.valueOf(node.right.data),node);
}
return true;
}
}
return false;
}
- 首先: 注意下参数
value和parent。我们想找到值等于该value的node,并且该node的父节点对于删除该node是至关重要的。 - 其次: 注意下返回值。我们的算法将会返回一个布尔值。我们的算法在找到并删除该节点时返回
true。否则返回false。 - 第2行到第9行:我们开始查找等于我们要查找的给定的
value的node。如果该value小于current node值,我们进入左子树,递归处理(当且仅当,current node有左孩子)。如果该值大于,则进入右子树。递归处理。 - 第10行: 我们开始考虑删除算法。
- 第11行到第13行: 我们处理了没有孩子、并且是父节点的左孩子的节点。我们通过设置父节点的左孩子为空来删除该节点。
- 第14行和第15行: 我们处理了没有孩子、并且是父节点的右孩子的节点。我们通过设置父节点的右孩子为空来删除该节点。
- 清除节点的方法:我将会在后续文章中给出 clear_node 的代码。该函数将节点的左孩子、右孩子和值都设置为空。
- 第16行到第18行: 我们处理了只有一个孩子(左孩子)、并且它是其父节点的左孩子的节点。我们将父节点的左孩子设置为当前节点的左孩子(这是它唯一拥有的孩子)。
- 第19行到第21行: 我们处理了只有一个孩子(左孩子)、并且它是其父节点的右孩子的节点。我们将父节点的右孩子设置为当前节点的左孩子(这是它唯一拥有的孩子)。
- 第22行到第24行: 我们处理了只有一个孩子(右孩子),并且是其父节点的左孩子的节点。我们将父节点的左孩子设置为当前节点的右孩子(这是它唯一的孩子)。
- 第25行到第27行: 我们处理了只有一个孩子(右孩子),并且它是其父节点的右孩子的节点。我们将父节点的右孩子设置为当前节点的右孩子(这是它唯一的孩子)。
- 第28行到第30行: 我们处理了同时拥有左孩子和右孩子的节点。我们获取拥有最小值的节点(代码随后给出),并将其值设置给当前节点。通过删除最小的节点完成节点移除。
- 第32行: 如果我们找到了要查找的节点,就需要返回
true。从第11行到第31行,我们处理了这些情况。所以直接返回true,这就够了。
- clear_node 方法:设置节点的三个属性为空——(value, left_child, and right_child)
/**
* 清空n节点
*
* @param node
*/
public void clearNode(BinaryTree node) {
node.data = null;
node.left = null;
node.right = null;
}
- find_minimum_value方法:一路向下找最左侧的。如果我们无法找到任何节点,我们找其中最小的
/**
* 查找树中最小值
*/
public Integer findMinValue(BinaryTree node) {
if (node != null) {
if (node.left != null) {
return node.left.findMinValue(node.left);
} else {
return Integer.valueOf(node.data);
}
}
return null;
}
原文链接:Everything you need to know about tree data structures
代码下载:
从我的 github 中下载,【译】数据结构中关于树的一切(java版)
推荐文章
🙂🙂🙂关注微信小程序java架构师历程 上下班的路上无聊吗?还在看小说、新闻吗?不知道怎样提高自己的技术吗?来吧这里有你需要的java架构文章,1.5w+的java工程师都在看,你还在等什么?